Case 2.2: KVLCC2 shallow water, trajectories
CASE 2.2: KVLCC2 manoeuvres in shallow water
1. Description of case 2.2
- KVLCC2 hull shape, at even keel draught of 20.8 meter (full scale), model scale draught 0.277m.
- LPP = 4.267 m (scale 75)
- No bilge keels.
- Free to move in all directions (although the roll angles will be small).
- Starting speed: Fn = 0.064 (corresponding to full scale 7 knots or model scale 0.415 m/s).
- Calm water
- g = 9.81 [m/s2], ρ=1000 [kg/m3]; ν=1.27×10-6 [m2/s]
- Propeller present and working at constant RPM. The RPM of the propeller is such that the ship is in (longitudinal) equilibrium at a speed of 7 knots full scale.
- Rudder (mariner type) steerable. The rudder rate will correspond to 2.32°/s on full scale or 15.68°/s on model scale
- GM is set to 5.64 meter (full scale), model scale value of 0.0752). The roll angle during the manoeuvres will be negligible, so it may not be needed to model this.
- Water depth is shallow water, Wd/T = 1.2
- Radius of gyration for yaw and pitch is 0.25LPP (in air)
- Radius of gyration for roll is 0.38B (in air)
Case 2.2 will consists of 2 3cases: case 2.2.1 (information about the self propulsion), case 2.2.2 (a 20/5 zig-zag test) and case 2.2.3 (a 35 turning circle test).
2. Experimental data
The submissions will be compared to model tests carried out by MARIN and FHR. These data are compared in a paper OMAE2015-42254 and OMAE2015-41912. Uncertainties have been defined in this paper.
3. Requested computations
3 types of information manoeuvres are requested. You can only deliver case 2.2.3 when you deliver case 2.2.2.
Table 1: overview of cases.
| Package |
Manoeuvre |
Starting speed V0 |
| Case 2.2.1 |
Self propulsion information |
Fn = 0.064 (equivalent to 7 knots full scale) |
| Case 2.2.2 |
20°/5° zig-zag test, starting to portside |
Fn = 0.064 (equivalent to 7 knots full scale) |
| Case 2.2.3 |
35° turning circle test, starting to portside |
Fn = 0.064 (equivalent to 7 knots full scale) |
The propeller RPM at t=0 should be such that the ship is in longitudinal equilibrium. So, for a CFD time domain simulations, the situation at t=0 is equivalent to a propulsion test! The analysers will look at this data.
Note regarding the length of the simulation. We understand that for time-domain CFD simulations, the computation time can be long. For simulations based on mathematical models this is not the case. But in order to perform a proper data analysis, the time trace needs to be sufficiently long. For the 20/5° zig-zag manoeuvre, at least including the second overshoot angle needs to be present (more when possible). For the 35° turning circle manoeuvre, at least a 360° turn has to be made
3.1 Submission 2.2.1: Self-propulsion
This submission is especially interesting for simulations based on URANS CFD. The result of this case is the equilibrium speed, the “neutral rudder angle”, and the RPM, in other words: the obtained longitudinal equilibrium (the propeller rpm and thrust). For simulations based on coefficient models, the neutral angle will often be zero.
- All results are to be given for model scale conditions.
- All simulations results should be provided in the format described in section 4.
- The propeller rate of revolution should correspond to the self-propulsion point of the model. When the RPM is unknown (because for example a constant thrust or actuator disk model is used in CFD based simulations) please indicate this.
- Similar to the experiment, the rudders should be controlled by following autopilot during course keeping:
 (2)
(2)
where δ(t) is rudder angle, proportional gain KP is 3.0, and the damping gain is 3 (on model scale) and 26 on full scale. ψC is the target yaw angle and ψ(t) is yaw angle. The maximum rudder rate should be assigned to 2.32 [deg/s] full scale or 15.68 [deg/s], model scale. Rudder angle should be controlled by P controller during approaching before starting rudder execution for manoeuvring (Target yaw angle: ψC=0°)
Please see section 5 for an example of the submission.
3.2 Submission 2.2.2: 20°/5° portside zig-zag manoeuvre
- All results are to be given for model scale conditions.
- All simulations results should be provided in the format described in section 4.
- The propeller rate of revolution should correspond to the self-propulsion point of the model. When the RPM is unknown (because for example a constant thrust or actuator disk model is used in CFD based simulations) please indicate this.
- Similar to the experiment, the rudders should be controlled by Equation (2) during approaching before starting rudder execution for starboard side zig-zag.
- During the zig-zag manoeuvre, the rudders should go to the real geometric 20 degrees (not to 20 degrees away from the neutral angle).
- The ship swops the rudder to the opposite side when the heading has achieved the values of 5°.
Please see section 6 for an example of the submission.
3.3 Submission 2.2.3: 35° portside turning circle manoeuvre
- All calculations are to be conducted for model scale conditions.
- All simulations results should be provided in the format described in section 4.
- The propeller rate of revolution should correspond to the self-propulsion point of the model. When the RPM is unknown (because for example a constant thrust or actuator disk model is used in CFD based simulations) please indicate this.
- Similar to the experiment, the rudders should be controlled by Equation (2) during approaching before starting rudder execution for starboard side zig-zag.
- During the turning circle manoeuvre, the rudders should go to the real geometric 35 degrees (not 35 degrees away from the neutral angle).
Please see section 7 for an example of the submission.
4. Format
Time series of the manoeuvres should be send to the organizers in an excel file. The data shall be give on model scale, and it will be compared to model scale data.
The submission consists of an excel file (example is given) with 17 columns and with rows for every time step. The time step is free to chose, but a small enough time step somewhere around 0.05 to 0.01 is recommended to get sufficient accuracy. The following quantities are asked:
| Symbol |
Item |
Unit |
| t |
time |
s |
| X |
X position in earth fixed system |
m |
| Y |
Y position in earth fixed system |
m |
| z |
z position in earth fixed system |
m |
| ϕ |
Roll angle |
degrees |
| θ |
Pitch angle |
degrees |
| ψ |
Yaw angle |
degree |
| u |
surge velocity in horizontal-body-fixed coordinate system |
m/s |
| v |
sway velocity in horizontal-body-fixed coordinate system |
m/s |
| w |
heave velocity |
m/s |
| p |
roll rate |
deg/s |
| q |
pitch rate |
deg/s |
| r |
yaw ratein body-fixed coordinate system |
deg/s |
| δ |
Rudder angle |
deg |
| n |
Propeller revolutions |
rpm |
| T |
Thrust of propeller |
N |
| Q |
Torque of propeller |
Nm |
| FR |
Rudder normal force (except horn part) |
N |
The sign convention is illustrated in Figure 1. The reference point is the origin, which is located at midships, the intersection of ordinate 10 the centre line plane and the still water waterline. There is a right-handed earth-fixed coordinate system x0y0z0 , and a horizontally moving right handed body-fixed coordinate system xyz. The body-fixed coordinate system has its origin in O, and the xy plane rotates with ship. These data are illustrated in Figure 1. The origin is located on O. The time t=0 is the time when the steering starts. The initial direction of the model is the direction of X-axis. Initial conditions at t = 0 are: X
0=0, Y
0=0, u=U
0, r=0, δ=δ
0 (which is the neutral rudder angle)
 Figure 1: sign convention
Figure 1: sign convention
Notes:
- The ship position or trajectory should be given in an Earth-fixed coordinate system with X pointing North, Y pointing East, and Z pointing downward as shown in Figure 1. This x0y0z0 axis system remains horizontal in the earth. The ship was released at (0,0) when t = 0 . The roll angle (ϕ) is positive for pushing starboard into the water, pitch (θ) is positive for bow up position and yaw angle (ψ) is positive for bow turned to starboard. The reported trajectory is dimensional and angular motions should be reported in degrees. The angular velocities should be reported in degree per second. The reported yaw angle should be the deviation of yaw angle respect to the target yaw i.e. ψ-ψC.
- All velocities for 6DOF motions (u, v, w p, q r) should be reported in ship-fixed coordinate system with x axis positive toward bow, y axis positive toward starboard and z axis positive downward. This xyz axis system rotates with the ship in yaw but not pitch and roll, i.e., remains horizontal in the earth. It is a so-called “yawed-only reference system”. Given this convention, the reported velocities are:
 (3)
(3)
 (4)
(4)
In Equation (4), the unit of p, r, 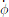 , and
, and 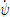 is [deg/s].
is [deg/s].
- Rudder angle (δ) is positive when trailing edge moves to portside.
- The thrust T and torque Q for each propeller should be reported in shaft coordinate system with x axis positive toward the engine. Values are given dimensional
- All motions should be reported at O.
- Link to excel file case 2.2.1, in which the submitter can put his data.
- Link to excel file case 2.2.2, in which the submitter can put his data.
- Link to excel file case 2.2.3, in which the submitter can put his data.
- Link to excel file, in which the submitter can put the details of the calculation method.
The yellow fields in the excel sheet should be filled in. The excel sheet should be send to the organizing committee per email address “
simman2019host@gmail.com”.
5. Example for case 2.2.1
For case 2.2.1, we will ask the equilibrium speeds u, v, the rudder angle, RPM (i.e. the neutral rudder angle), thrust and torque, when available in the used method.
6. Elaborated example for case 2.2.2 (20/5 zig-zag test, starting to portside)
For case 2.2.2, the time traces will be gathered and a comparison will look as displayed in the following figure 2. As can be seen, the results of the time traces will be post-processed and presented non-dimensional. Additionally to the figure 2, the values of overshoot angles, rates of turn, period, etc will be derived from the time series. Table 3 illustrated which characteristics will be derived from the time series. These will be compared too as displayed in the below figure 3 for one submission compared to the FRMT data. A statistical analysis will be performed for all submissions to observe the spreading in results.
The primary values for the comparison will be the rates of turn and the period. The secondary values for the comparison will be the overshoot angles.
Table 3: Comparison values for Case 2.2.2
| Category |
Unit |
Validation Variables |
| Overshoot angles |
[deg] |
1st overshoot angle (ψOS1) |
|
[deg] |
2nd overshoot angle (ψOS2) |
|
[deg] |
3nd overshoot angle (ψOS3) |
| Time of execute |
[s] |
Time of 2nd rudder execute (t2) |
|
[s] |
Time of 3rd rudder execute (t3) |
|
[s] |
Time of 4th rudder execute (t4) |
| Times |
[s] |
Period (time between the 4th and 2nd rudder execute = t4-t2) |
|
[s] |
1st overshoot time (tOS1) |
|
[s] |
2nd overshoot time (tOS2) |
|
[s] |
3rd overshoot time (tOS3) |
| Maximum yaw rate |
[deg/s] |
Maximum yaw rate during 1st overshoot between t2 and t3 (r1) |
|
[deg/s] |
Maximum yaw rate during 2nd overshoot between t3 and t4 (r2) |
|
[deg/s] |
Maximum yaw rate during 3rd overshoot between t4 and t5 (r3) |
| Maximum drift angle |
[deg] |
Maximum drift angle during 1st overshoot between t2 and t3 (β1) |
|
[deg] |
Maximum drift angle during 2nd overshoot between t3 and t4 (β2) |
|
[deg] |
Maximum drift angle during 3rd overshoot between t4 and t5 (β3) |
 Figure 2: time traces of several submissions for the 20/5 zig-zag manoeuvre, compared to FRMT
Figure 2: time traces of several submissions for the 20/5 zig-zag manoeuvre, compared to FRMT
 Figure 3: comparison of derived characteristics.
Figure 3: comparison of derived characteristics.
7. Elaborated example for case 2.2.3: 35° turning circle manoeuvre to portside
For case 2.2.3, the comparison will look as displayed in the following figure 4 and 5. As can be seen, the results of the time traces will be analysed and presented non-dimensional. On top of the time traces as presented in figure 4 and 5, the values of tactical diameter, rate of turn, drift angle, speed loss, etc will be derived from the time series. Table 4 illustrated which characteristics will be derived from the time series. These characteristics will be compared too as displayed in the figure 6: this shows how a submissions is compared to the FRMT data. A statistical analysis will be performed for all submissions to observe the spreading in results.
The primary values for the comparison will be the rate of turn and drift angles. The secondary values for the comparison are indicated in the table 4.
Table 4: Comparison values for the 35° turning circle manoeuvre
| Category |
Unit |
Validation Variables |
| Dimensions |
[-] |
Advance / LPP (Ad/LPP) |
|
[-] |
Tactical diameter / LPP (TD/LPP) |
|
[-] |
Transfer / LPP (Tr/LPP) |
| Times |
[s] |
Time to reach 90° (t90°) |
|
[s] |
Time to reach 180° (t180°) |
|
[s] |
Time to reach 36° (t360°) |
| Yaw rate |
[deg/s] |
Maximum yaw rate (rmax) |
|
[deg/s] |
Average yaw rate in the constant part of the turn (rC) |
| Speed |
[m/s] |
Speed in the steady part of the turn (UC) |
| Non-dimensional values |
[-] |
Non-dimensional yaw rate in the constant part of the turn (r’) |
|
[deg] |
Drift angle in the constant part of the turn (βC) |
|
[-] |
Pivot point (-sin(βC)/r’) |
|
[-] |
Speed ratio (UC/U0) |
 Figure 4: Time trace of signals
Figure 4: Time trace of signals
 Figure 5: bird-eye plot
Figure 5: bird-eye plot

Table 3: comparison of derived characteristics between the submission and two experimental values.
 (2)
(2)
 (3)
(3) (4)
(4)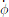 , and
, and 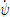 is [deg/s].
is [deg/s].




